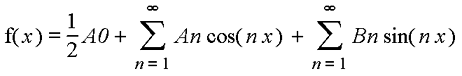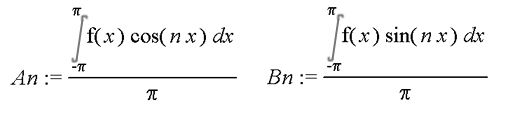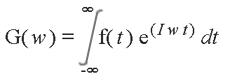|
 |
 |
Compressioni Audio
MP3 & SoundVQ
Non vi é alcun dubbio che la Rete abbia aiutato la sopravvivenza
e la nascita di nuovi standard audio/video. Uno di questi é MP3,
un nuovo formato per la compressione audio, che sta vivendo un momento
di grande successo e notorietá. Altri formati si stanno affacciando,
e il piú promettente fra questi é il SoundVQ di Yamaha. In
questo articolo prenderemo in esame entrambi.
di Cristiano Paris e Luciano Liberati
Provate ad inserire la parola MP3 nel vostro
motore di ricerca preferito : noi lo abbiamo fatto su Altavista e il risultato
é stato impressionante : 280 mila link. Ma che cosa é MP3
? L'acronimo indica la terza versione del formato di compressione utilizzato
nelle codifiche MPEG1 ed MPEG2. ovvero l'MPEG Audio Layer 3. In effetti
MP3 ha conquistato il suo meritato successo grazie alle superbe prestazioni
e alla gratuitá della tecnologia impiegata. I dati forniti dal consorzio
MPEG in tal senso sono sconcertanti : fino a 15 ore di audio in qualitá
CD e fino a 60 ore di parlato su singolo CD-ROM. Queste caratteristiche
hanno dato il via a tutta una serie di applicazioni, tra le quali spicca
la distribuzione via Internet di intere tracce audio in qualitá
CD. Purtroppo, a parte qualche caso isolato, il resto dei siti che operano
in tal senso, lo fá nella completa illegalitá, tanto che
le major si stanno mobilitando per fermare questo ingente traffico e attuare
manovre repressive.
In effetti l'utilizzo massiccio di MP3 nel contesto internettiano rassomiglia
all'invenzione delle fotocopie per i documenti cartacei, solo che stavolta
le fotocopie sono praticamente identiche all'originale.
Inoltre, come dicevamo, lo standard MP3 é completamente free,
e i suoi algoritmi di codifica sono accessibili a chiunque, rendendo cosí
difficile la messa a punto di una regolamentazione sulla base unicamente
di vincoli al software di codifica/decodifica, come invece sta accadendo
con il DVD.
Questa pecca di MP3 potrebbe rivelarsi decisiva per i nuovi standard
che cominciano ad affacciarsi sul mercato. Il piú promettente tra
questi é senz'altro il SoundVQ di Yamaha, formato che andremo ad
analizzare in questo articolo.
Inoltre il consorzio MPEG sta preparando un nuovo formato audio che
verrá incluso nel nuovissimo standard MPEG4, e che promette grandi
migliorie, soprattutto sotto il punto di vista della distribuzione real-time
e stream dei dati audio/visivi.
Forme d'onda
In questo e nei prossimi due paragrafi cercheremo di introdurre alcuni
dei concetti teorici che si trovano dietro MP3 e SoundVQ. Si tratta di
concetti molto complessi, che riguardano l'analisi di Fourier e la quantizzazione
vettoriale. Tuttavia, il nostro scopo é lontano dalla rigorosa trattazione
matematica, e indirizzeremo la nostra attenzione verso i concetti importanti
di questa tecnologia.
Tutti sanno che il suono é una entitá fisica che si basa
sul concetto di onda, che all'atto
pratico é una specie di vibrazione. Ora, ogni suono induce vibrazioni
diverse sul mezzo che ne é preposto alla ricezione, come per esempio
un microfono o l'orecchio. Quindi, per registrare il suono, vorremmo saper
descrivere la vibrazione che esso induce. Per far questo utiliziamo il
concetto matematico di funzione. Un'onda sonora é in pratica una
funzione del tempo, perché essa descrive la vibrazione al variare
del tempo (in realtá essa é anche funzione dello spazio,
ma noi assumeremo di descrivere la vibrazione in un determinato punto dell
spazio, eliminando questa scomoda variabile).
L'onda sonora piú semplice che possiamo immaginare é
l'onda armonica, che ha questa forma :
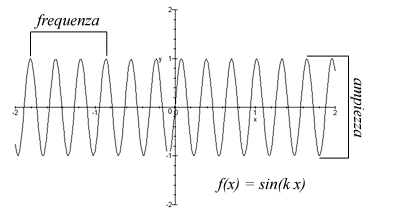
Come vedete si tratta di una serie ininterrotta di onde che salgono
e scendono. Se poteste inserire questa funzione nel vostro computer, sentireste
un tono continuo, che riproduce sempre la stessa nota.
Ora, un'onda armonica possiede alcune caratteristiche la rendono unica.
Esse sono la frequenza e l'ampiezza. Osserviamo la seguente figura
:
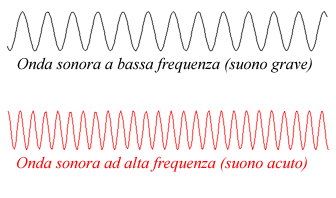
Nella prima vediamo che le onde sono piú diradate rispetto alla
seconda. Questo significa che la prima onda possiede una frequenza piú
bassa rispetto alla seconda, con una conseguente variazione della nota
riprodotta : la prima sará piú grave rispetto alla seconda.
La frequenza si misura in Hertz (Hz) e, come abbiamo visto, tanto é
piú grande, tanto piú la nota riprodotta sará acuta.
La seconda carateristica, l'ampiezza, rappresenta l'altezza che le
ondine posseggono : piú questa altezza é grande, piú
il suono avrá un volume elevato.
Supponete adesso di avere due onde armoniche di diversa frequenza,
che quindi riproducono due note diverse, e supponete di volerle suonare
contemporaneamente. Per fare questo non dovete fare altro che sommare,
istante per istante, le due forme d'onda, che si combineranno quindi in
una nuova onda. Vediamo come avviene questo processo :
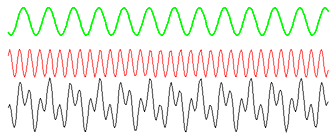
Come vedete, l'onda risultate ha una forma molto strana, dovuta alla
somma delle due onde originali. In effetti le onde sonore assumono di solito
forma ben piú strana ed imprevedibile. Tuttavia esse possono essere
sempre ricondotte alla somma di forme d'onda piú semplici. Ed é
da questa considerazione che Fourier inventó l'analisi armonica,
di fondamentale importanza nella moderna teoria dei segnali. Vediamo come
funziona.
La considerazione di Fourier ci dice che qualsiasi onda sonora, di
qualsiasi forma essa sia, puó essere pensata come la somma di un
certo numero di onde sonore piú semplici, le onde armoniche, di
diversa ampiezza e frequenza. Fourier diede anche una formula che riassume
questo concetto :
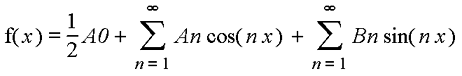
Ai piú questa formula potrá sembrare incomprensibile,
eppure il suo significato é molto intuitivo. Notiamo innanzitutto
che il numero di onde sonore da sommare é infinito : questa é
una condizione imprescindibile, che peró puó essere aggirata
utilizzando delle approssimazioni.
Che cosa andiamo a sommare ? Le funzioni sin e cos rappresentato
proprio le armoniche, ovvero le onde sonore fondamentali. Le frequenza
di tali armoniche é data dalla n che compare nell'argomento
di sin e cos. Notiamo quindi che queste frequenze sono fisse
: 1, 2, 3 ecc. Non ci sono mezze vie. L'analisi di Fourier infatti, tiene
in considerazione solo alcune onde armoniche che vengono definite fondamentali.
L'ampiezza di queste onde armoniche fondamentali é rappresentata
dai coefficienti An e Bn. Piú questi valori sono alti, piú
l'armonica corrispondente sará preponderante nel suono.
Fourier ha dato anche le formule per questi due coefficienti. Esse
sono :
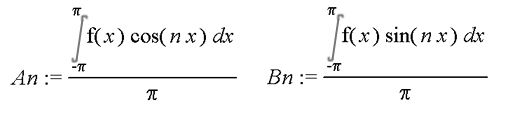
Non vi spaventate, non andremo a risolvere questi integrali.
Un esempio a questo punto mi pare necessario. Supponiamo che l'onda
sonora che vogliamo analizzare corrisponda proprio ad una armonica fondamentale,
ad esempio la quinta. Se utilizziamo le formule integrali di Fourier per
determinare i coefficienti ci accorgeremo che questi sono tutti nulli,
tranne il quinto. Questo ci dice che il suono é formato da una sola
armonica fondamentale : la quinta. Ed é proprio cosí infatti,
visto che il suono analizzato corrisponde proprio proprio alla quinta armonica.
Questo esempio é di fondamentale importanza. Infatti, un suono
puó essere rappresentato sia attraverso la sua forma d'onda che
attraverso la sua rappresentazione di Fourier. Quest'ultima peró
offre un vantaggio netto sulla prima : essa puó essere compressa
molto piú efficacemente, in quanto é sostanzialmente
una sequenza quasi ininterrotta di zeri.
Vediamo quindi come la rappresentazione di Fourier sia estremamente
vantaggiosa.
Supponiamo ora di combinare due diverse onde armoniche fondamentali,
ad esempio la quinta e l'ottava. Allora tutti i coefficienti di Fourier
saranno nulli, tranne, ovviamente, il quinto e l'ottavo.
Un esempio un pó piú complesso é il seguente,
in cui utilizziamo un'onda quadra :
A1 = 1,683
A2 = 0,91
A3 = 0,094
...
A160 = 0,002
Come vediamo, in questo caso i coefficienti di Fourier sono tutti diversi
da zero, ma diventano sempre piú piccoli man mano che le armoniche
crescono (per n che diventa grande). Da un certo punto in poi, queste
armoniche diventeranno pressoché impercettibili all'orecchio umano,
tanto da poter essere eliminate dalla rappresentazione di Fourier.
In casi reali, gran parte dei coefficienti risultano molto piccoli
(il suono possiede frequenze localizzate in bande precise), tanto da poter
essere completamente eliminati senza che il segnale subisca degradazioni
di alcun genere, e generando una successione di valori quasi tutti nulli
e quindi altamente comprimibile.
Trasformate di Fourier
Il problema dell'analisi di Fourier che abbiamo descritto é che
essa é limitata a suoni periodici e ripetitivi, al contrario di
quanto succede nel mondo reale. Per superare questa difficoltá,
Fourier estese gli integrali che definiscono i coefficienti An e Bn a tutto
il campo reale. Inoltre, all'interno di quegli integrali, sostituí
la variabile n, che assume solo valori discreti, con la variabile
w, che invece puó assumere qualsiasi valore continuo. Ancora,
utilizzando le definizioni di Eulero per l'esponenziale complesso, cambió
le due serie in :
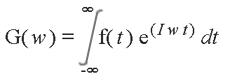
Non spaventatevi ! Il fatto che esso sia un integrale complesso esteso
a tutta la retta reale interessa poco, in quanto il suo calcolo puó
essere automatizzato con degli algoritmi molto efficaci come la Fast Fourier
Transform. Quello che invece ci interessa é che il suo valore ci
dice quanto é prominente la frequenza w nel suono f(t).
Potete quindi immaginare la traformata di Fourier come un'operazione
trasforma il suono, che, lo ricordiamo, descrive una vibrazione nell'arco
del tempo, in uno spettro, che non é nient'altro che l'insieme
delle frequenze contenute in un suono.
Vediamo ad esempio come si presenta la trasformata di Fourier di un'onda
quadra :
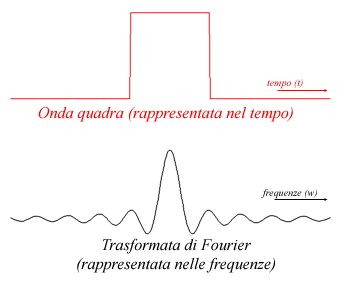
Come vedete, lo spettro delle frequenze contenute nell'onda quadra
é in generale diverso da zero, ma allontanandoci dall'origine, queste
tendono a diminuire di ampiezza e a diventare insignificanti, tanto da
poter essere eliminate.
Inoltre si é constatato che l'orecchio umano é sensibile
sono ad un certo intervallo di frequenze (detto campo dell'udibile), al
di fuori dei quali troviamo per esempio gli ultrasuoni. Inoltre, all'interno
di questo intervallo, l'orecchio umano é piú sensibile a
determinate frequenze rispetto ad altre, che quindi possono venire maggiormente
approssimate, senza che il suono perda la sua qualitá.
Possiamo poi fare un'altra osservazione. Supponiamo di avere un'onda
quadra e un'onda armonica. Si puó tarare l'onda quadra in maniera
che essa emetta la stessa nota dell'onda armonica. Tuttavia le trasformate
di Fourier di queste due onde sonore saranno sostanzialmente differenti
: questo ci induce a pensare che la trasformata di Fourier sia una specie
di carta d'identitá di una qualsiasi onda sonora, un parametro che
integra la frequenza e l'ampiezza, che erano invece peculiare solo alle
onde armoniche. In effetti questo concetto é legato a quello ben
piú importante di timbro.
Un clarinetto e una tromba possono suonare la stessa nota, ma i due
suoni saranno diversi, in quanto posseggono due timbri diversi. In effetti
la voce umana potrebbe essere pensata come uno strumento musicale (pensate
al canto) che possiede un proprio timbro. Attraverso l'analisi armonica
é possibile analizzare questo timbro e constatarne le caratteristiche.
Inoltre, se sappiamo in anticipo quale sará il timbro del suono
in questione, potremmo per esempio ignorare determinate frequenze che sappiamo
essere trascurabili nel timbro e ottenere una rappresentazione estremamente
compatta e comprimibile del suono.
Come abbiamo detto l'analisi di Fourier é la base matematica
utilizzata nell'MP3, ma essa viene efficacemente impiegata anche nella
codifica JPEG ed MPEG.
Quantizzazione Vettoriale
Il SoundVQ di Yamaha invece utilizza una diversa teoria : la Vector Quantization
o VQ, da cui il nome. Quest'ultima é senz'altro piú complessa
della prima, quindi ne daremo solo un breve accenno.
Per chiarire le idee, supponete di avere un piano su cui sono disegnati
dei puntini. In generale i puntini possono assumere qualsiasi posizione,
ma noi supporremo per convenienza che la loro distribuzione non sia casuale.
Supponete ora di dividere lo spazio in tante zone chiamandole con delle
lettere. A questo punto cominciate a numerare i puntini che avete disegnato.
A prima vista é molto semplice dire che il puntino numero n
appartiene alla zona X. Tuttavia, per complicarci la vita, inseriamo
altri puntini, questa volta rossi, uno per ogni zona. Avremo quindi il
puntino rosso A, il puntino rosso B, il puntino rosso C ecc.
I puntini rossi peró non sono posizionati a caso nella zona
: essi rispettano una importante proprietá. Supponete ad esempio
che il puntino nero numero 4 appartenga alla zona B. Allora, il puntino
rosso B é quello che dista meno dal puntino nero numero 4, rispetto
agli altri puntini rossi. E cosí anche per gli altri.
La situazione é quella descritta in figura :
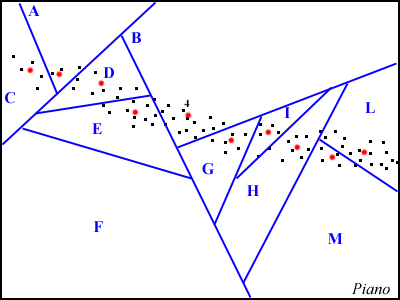
Il risultato é quello di aver approssimato la distribuzione dei
puntini neri con i puntini rossi. Se i puntini rossi sono in numero sufficiente,
operare sui puntini rossi o su quelli neri non fá una grande differenza.
Questo principio é di grande importanza per la compressione
sonora. Infatti, si puó pensare ogni punto del piano come una frequenza
del suono da comprimere, quindi suddividere in zone tale piano (creando
dei domini di frequenza) e applicare la quantizzazione vettoriale per approssimarne
la distribuzione (dove l'approssimazione sará piú grossolana
in domini di frequenza molto grandi, ovvero in zone di frequenze a cui
l'orecchio non é molto sensibile). In generale il numero di puntini
rossi sará minore dei puntini neri, diminuendo quindi la complessitá
del segnale in favore di una maggiore compressibilitá.
Trovare le posizioni di ciascun puntino rosso non é comunque
cosa facile, e gli algoritmi utilizzati sono molto complicati (esistono
interi corsi universitari per questo). Spesso comunque si é osservato
come le reti neurali (in particolare le reti di Kohonen) siano un'ottima
soluzione per questo tipo di problemi.
In pratica
Prima di cominciare la nostra carrellata di codificatori e player per Windows95
ed NT, vorrei spendere una parola sulle prestazioni che essi offrono e
sulle loro caratteristiche.
Diciamo innanzitutto che sia MP3 che SoundVQ offrono una qualitá
paragonabile a quella CD solo se vengono rispettate determinate condizioni.
La prima di queste riguarda la frequenza di campionamento del segnale in
ingresso. Entrambe le codifiche prevedono varie possibilitá, ma
esse danno il meglio sono quando tale frequenza é uguale o superiore
ai 44 Khz. Sotto questa frequenza, le codifiche degradano sensibilmente
il segnale, in quanto numerose frequenze utili vengono escluse a priori
dalla codifica.
La seconda condizione é il bit-rate, ovvero il numero di bit
che vengono impiegati per rappresentare un secondo di audio. Lo standard
precedente, MP2, prevedeva un bit-rate di 128Kbit/sec per la qualitá
CD, mentre lo standard MP3 riduce questa necessitá a 112/96Kbit/sec.
Si tratta di bit-rate molto bassi, che permettono un rapporto di compressione
pari a 10:1 e 12/15:1. Tuttavia, SoundVQ riduce ancora tale richiesta,
scendendo persino a 80Kbit/sec e portando il rapporto di compressione a
17:1.
In ogni caso é lo standard MP3 che offre una maggiore versatilitá,
essendo il suo formato libero da qualsiasi vincolo legale, a differenza
del SoundVQ, che attualmente é supportato solo dalla Yamaha.
I programmi testati seguenti:
-
l3enc : uno dei primi nati per la codifica/decodifica mp3.
-
l3enc/win : un front-end per l3enc.
-
Mpeg Encoder : altro encoder per Windows
-
Mp3 Compressor : molto semplice da usare ed estremamente veloce
-
Winamp : la rolls-royce dei player di mp3
-
SoundVQ suite : encoder e player in formato vqf
Vediamoli in dettaglio.
l3enc 2.71
Rappresenta senz'altro l’approccio più completo nei confronti
dell’mp3. Nella sua versione shareware, permette con pochi passaggi di
convertire un file WAV-PCM nel corrispondente MP3. Altri formati consentiti
sono : l'immancabile RAW, l'AIFF/AIFC (utilizzato dal Mac), il SND e il
canonico AU (diffuso su piattaforme NeXT e Sun, ma ormai comune nelle nostre
navigazioni quotidiane).
Nella versione non registrata permette di comprimere solo con una sampling
frequency pari a 44.1 Khz, comunque utile per testare subito le potenzialità
del prodotto.
Necessario leggere il manuale allegato al software prima di iniziare,
proprio a causa della completa assenza di una interfaccia grafica; le opzioni
sono molte, ma quelle per iniziare sono abbastanza chiare: basta inserire
il nome del nostro file sonoro (che nella versione non registrata sarà
necessariamente di tipo .snd/.wav/.aiff.), quello in output e il gioco
è fatto. Ovviamente bisognerá attendere che il programma
completi la codifica, che si rivela un processo lungo, soprattutto per
processori poco dotati.
Leggendo il manuale ci si accorge poi della quantità industriale
di opzioni presenti: si va dalla scelta del bitrate, alla possibilità
di comprimere in versione “high quality” (tempi di attesa quasi quintuplicati),
di miscelare un segnale stereo e trasformarlo in mono, di inserire informazioni
ausiliare, la possibilità di ottimizzare la compressione nel caso
di massiccia presenza di parlato, ed opzioni specifiche per utenti che
utilizzano formati diversi da quelli di windows.
Inoltre l3enc sceglie automaticamente tra MP2 ed MP3, a seconda del
bitrate che si è scelto. Comodo infine l’indicatore dei frames compressi
e il numero di quelli da comprimere, in modo da avere sotto controllo la
situazione.
l3enc/win 2.01
Si tratta di un pratico front-end per gli utilizzatori di l3enc. L’uso
è quindi semplicissimo : unica accortezza è quella di aggiungere
la directory di l3enc nel PATH di autoexec.bat.
Nonostante questo programma sia giunto alla versione 2.01, le opzioni
offerte sono esigue. E' possibile selezionare il bitrate da un comodo menù,
scegliere di cancellare il wave dopo la compressione e decidere di miscelare
i due canali stereo per ottenerne uno mono.
Fatto questo basta scegliere il file di partenza, la directory di arrivo
e premere il pulsante RUN per vedersi aprire una finestra dos dove
viene eseguito l3enc in modo assolutamente automatico.
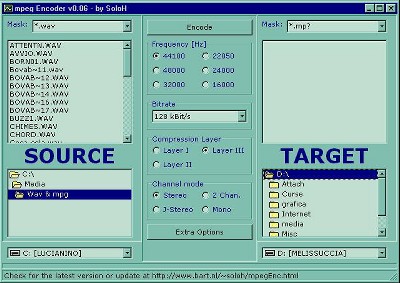
Mpeg Encoder 0.06 (http://users.bART.nl/~soloh/mpegEnc.html)
Programma molto ben fatto ma dalle caratteristiche un po’ anomale: infatti,
a un interfaccia veramente intuitiva contrappone una lentezza esasperante
nella codifica.
Comunque con pochi click possiamo selezionare il bitrate e la frequenza
voluta, il tipo di compressione (MP1, MP2 o MP3) e, al solito, scegliere
il numero dai canali da utilizzare. Un menù apposito ci da poi la
possibilità di accedere alle opzioni avanzate, tra cui spiccano
l’effetto enfasi, le informazioni da associare al file, la priorità
con cui il programma deve girare, una curiosa opzione che permette di selezionare
la psicoacustica desiderata ecc. Avviata la compressione, una comoda barra
ci peremtte di tenere la situazione sotto controllo. Non è presente
un help in linea, ma solo un file in formato testo che spiega determinate
operazioni.
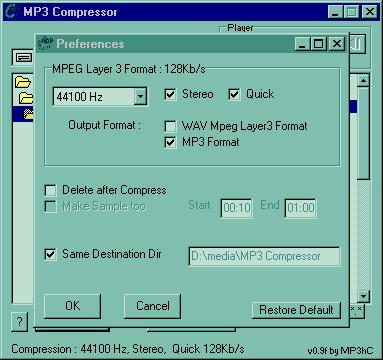
Mp3 Compressor 0.9f
Godendo di un codice ottimizzato per Win32, il programma offre una velocitá
pressoché tripla rispetto all’l3enc. Unico difetto : opzioni troppo
carenti. In ogni caso, trattandosi di una versione non definitiva, possiamo
sperare che la situazione migliori. Tutta l’operazione di compressione
si limita a selezionare la frequenza (il bitrate è automaticamente
settato a valori ottimali), scegliere il WAV e attendere che il programma
porti a termine il suo compito. Inoltre, durante l’elaborazione è
possibile settare la priorità del programma al massimo, escludendo
Win95 (Windows NT invece rimane vigile) e riducendo le indicazioni "in
progress" al minimo.
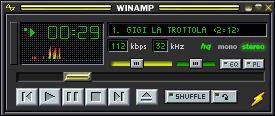
Winamp 1.73 (http://www.winamp.com)
Il miglior player attualmente presente sul mercato. Richiede pochissimo
spazio su HD (meno di 600 Kb) a fronte di un'offerta di opzioni e versatilitá
veramente impressionante. Un interfaccia intuitiva e curata ci permette
di scegliere l’mp3 da ascoltare, dandoci ad esempio la possibilità
di equalizzare il segnale o di creare una playlist (una lista dei nostri
brani preferiti, ascoltabili secondo la seguenza che più ci aggrada).
Progettato secondo un'interfaccia simile ad un componente stereo HiFi,
consente tutte le operazioni tipiche di un lettore CD, come la ripetizione
dei brani, la riproduzione casuale delle tracce ecc. L'equalizzatore poi
é disponibile il due versioni : la classica e la fiammeggiante (vi
lasciamo indovinare cosa significhi).
Ma se è la spettacolarità che ci interessa, posiamo utilizzare
uno dei numerosissimi plug-in studiati per Winamp, che aggiungono nuove
capacità al nostro player preferito.
Alcuni di questi sono cosí sofisticati da richiedere la presenza
di una scheda 3dfx, offrendo un impatto visivo veramente spettacolare.
Tra i più diffusi ci sono gli analizzatori di spettro e di livello,
digitali ed analogici. Alcuni si integrano direttamente nell’interfaccia
di Winamp, mentre altri aprono una propria finestra separata, o addirittura
occupano l'intero schermo (come nel caso dei plug-in per 3dfx). Uno dei
plug-in più curiosi è quello che permette di comandare Winamp
tramite il nostro joystick. Ce ne sono veramente di tutti i tipi ed il
loro utilizzo è molto semplice : basta copiare alcuni file nella
directory di Winamp e selezionarli successivamente in un comodo menù
da dove è anche possibile configurarli.
[NOTA : Al momento della pubblicazione é stata recentemente
rilasciata la versione 1.90 che permette la modifica della grafica del
pannello, denominata skin. Inoltre, da questa versione Winamp diventa shareware,
durando solo 14 giorni]
SoundVQ Suite Beta 2 (http://www.yamaha.co.jp)
La suite presentata da Yamaha é composta da un encoder e da un
player. La versione da noi provata risulta essere una Beta non definitiva.
Nonostante ció il software non ha mai dato problemi e l'installazione
é stata precisa ed accurata, anche se un pó spartana.
L'encoder, disegnato per Windows, propone tutte le opzioni configurabili
in una singola schermata. Come al solito si puó scegliere il file
WAV da comprimere e il corrispettivo file VQF prodotto. In entrambi i casi
si puó ascoltare il file selezionato per avere una comoda preview.
E' possibile scegliere quindi il bit-rate (che é limitato a due
sole possibilitá), il numero di canali e la qualitá di compressione
(Low, Normal o High) che influirá sulla velocitá di codifica.
Infine é possibile settare alcune info nel file da comprimere e
la possibilitá di impedire all'utente finale di risalvare il file
all'interno del player (probabilmente per evitare il diffondersi di copie
illegali).
Il player invece, che come al solito é stato sviluppando pensando
ad un componente HiFi, offre un'interfaccia accattivante, ma risulta carente
sotto il profilo dell'operabilitá. Comunque assolve egregiamente
alla sua funzione.
Da notare che l'installazione provvede ad installare un plug-in per
Netscape con il quale é possibile ascoltare file VQF, anche in versione
stream.
Benchmark
Per effettuare i benchmark ci siamo serviti di un K6-200Mhz su motherboard
Asustek e 32 Mb di SIMM ram (60 ns). Abbiamo codificato la traccia audio
di un CD contenente la fanfara della 20th Century Fox, modificata per non
infrangere il copyright vigente. La lunghezza del WAV originale era di
3.26MB, per un totale di 19.4 secondi a 44.1Khz stereo 16-bit. Abbiamo
codificato tale traccia con SoundVQ, MP3 Compressor e l3enc, ottenendo
i seguenti risultati :
-
SoundVQ : 44.1 Khz a 80Kbit/s in High Quality. 189Kb in 3 min e 31 sec.
-
MP3 : 44.1 Khz a 128 Kbit/s. 302Kb in 27 sec.
-
l3enc : 44.1 Khz a 112 Kbit/s. 265Kb in 1 min e 20 sec.
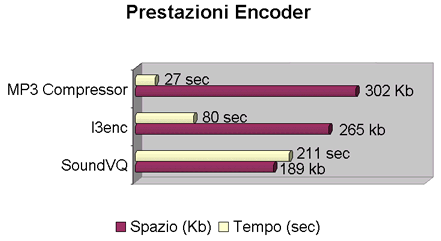
Come vediamo il formato VQF offre una minore occupazione (189Kb contro
i 302Kb di MP3), con un rapporto di compressione pari a 17,7 : 1. Tuttavia
il coder di Yamaha é senz'altro il piú lento, a causa forse
dell'accresciuta complessitá algoritmi di codifica.
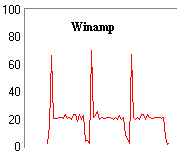
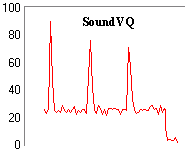
Abbiamo poi misurato l'occupazione percentuale del processore dei due
player, Winamp e SoundVQ, utilizzando il monitor di Windows NT. Ecco i
due grafici relativi a tre ripetizioni dello stesso brano :
Come vediamo, in media, l'occupazione del processore é di circa
il 20%, insoddisfacente per un ascolto in background, ma piú che
ottima se il player é il task principale.
I picchi, che denotano l'inizio di ogni ripetizione, sono dovuti, con
ogni probabilitá, alla fase di pre-codifica, che consente di evitare
qualsiasi interruzione nel flusso dei dati, qualora questo venissero attinti
da periferiche a flusso non costante, come accade per esempio in situazioni
di uso in background.
___________________
NOTA: I due file utilizzati per la prova sono disponibili
presso il sito di Beta. Fate click qui per andarci
Cristiano Paris studia Ingegneria Informatica presso la II Universitá di Roma
"Tor Vergata". Articolista di BETA dal 1995 si occupa di compressione e trattamento
dei segnali digitali. I suoi interessi spaziano anche nella crittografia e
nell'intelligenza artificiale. Cristiano è
raggiungibile su Internet tramite la redazione.
Luciano Liberati studia Ingegneria Meccanica presso la II Universitá di Roma "Tor Vergata".
|