
CRITTOGRAFIA
UNA NECESSITÀ
Internet é senza dubbio un formidabile mezzo di comunicazione.
Grazie ad esso le distanze si riducono ed i popoli si avvicinano. Purtroppo,
anche Internet ha i suoi punti deboli ed il piú famoso é
senza dubbio la sicurezza. Vediamo insieme in quest'articolo come difendere
i nostri dati da sguardi indiscreti e da pericolose riesumazioni del "Grande
Fratello"
di Cristiano Paris
Per capire quali sono i problemi relativi
alla sicurezza su Internet, occorre innanzitutto compiere un excursus sulla
sua struttura e sul suo funzionamento. Internet nacque venti anni fa come
esperimento dell'ente della difesa statunitense ARPA: all'epoca infatti,
la sua denominazione fu appunto Arpanet. Il suo scopo era quello
di fornire un sistema di comunicazione fra i punti vitali delle istituzioni
americane [establishment, difesa, centri di coordinamento] che fosse in
grado di resistere ad un eventuale attacco nucleare da parte della coalizione
filo-sovietica. Gli scienziati svilupparono cosí una filosofia di
connessione completamente nuova e rivoluzionaria a cui venne dato il nome
di "rete a commutazione di pacchetto" [packet switching network,
PSN]. Il nome nasconde un sistema di trasmissione delle informazioni semplice
ma geniale; per capirlo, osserviamo la figura seguente :
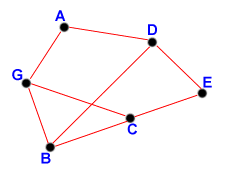
Una tipica rete PSN [Packet Switching Network] di sei nodi
Ad una prima occhiata, le connessioni fra i vari computer [nodi] non
sembrano rispettare alcuna logica precisa, come invece avviene nelle reti
tradizionali [token ring, rete centralizzata e cosi' via]. Tuttavia ció
non rappresenta necessariamente uno svantaggio. Ammettiamo infatti di voler
spedire un messaggio [pacchetto di dati] dal computer G al computer E.
Nel far questo assumeremo che tutti i collegamenti siano bilaterali (non
sempre é cosí : molte connessioni, come il feeding via satellite
di molti news server, sono unilaterali). In una rete tradizionale, le informazioni
percorrono sempre lo stesso tragitto all'interno della rete. Questo invece
non é sempre vero in una rete PSN. Viene infatti introdotta una
fase prelimanare alla trasmissione dei dati che viene definita "routing"
[tracciamento del percorso]. In tale fase il protocollo prevede che venga
tracciato un percorso tra i vari nodi della rete in modo che il nodo G
e il nodo E siano messi in comunicazione. Ve ne potete accorgere quando
su un qualsiasi browser WWW lanciate una richiesta di collegamento ad un
sito remoto : ad esempio su Navigator, il browser sentenzia "Contacting
host..."; questo significa che si sta tentando di tracciare un percorso
che conduca i dati dal vostro computer al server a cui volete collegarvi.
Quando il browser finalmente risponde "Host contacted. Waiting for
reply", significa che il percorso é stato tracciato e che é
pronto per ricevere i dati. Oppure potete provare a dare il comando "tracert
www.beta.it" in una finestra DOS di Windows 95 o in una shell Unix, dove
il comando questa volta é traceroute.
Cosí, nel nostro caso, un possibile percorso é G-C-E (é
il meno costoso in termini di nodi attraversati). Ammettete ora che il
nodo C sia fuori uso. In tal caso la rete é ancora in grado di trovare
un percorso valido, ovvero G-A-D-E. Come potete ben immaginare, qualora
anche il nodo D fosse fuori uso, la rete non sará piú in
grado di mettere in comunicazione G con E. Ovviamente, in una situazione
reale, la rete viene sviluppata per soddisfare determinate necessitá,
come ad esempio la possibilitá di collegarsi ad un nodo con un numero
molto elevato di percorsi, e in definitiva in modo tale che il numero medio
di percorsi possibili tra due nodi sia il piú elevato possibile.
Questo ovviamente si risolve in una piú complessa progettazione
di una rete PSN rispetto alle reti tradizionali a schema fisso, tant'é
che il mercato delle applicazioni che aiutano il progettista a disegnare
le connessioni in una rete PSN é estremamente fiorente.
Purtroppo, una simile versatilitá si paga in termini di minore sicurezza.
Nell'attraversare i nodi C, A e D, il pacchetto di dati sará visionabile
da chiunque abbia accesso ai suddetti terminali, anche sistematicamente.
E' noto ad esempio che il governo cinese abbia deciso di far passare tutti
i collegamenti ad Internet attraverso il server del ministero dell'interno,
cosí da essere in grado di monitorare l'attivitá di ogni
cittadino, limitandone fortemente la libertá di espressione.
La situazione non é comunque cosí critica, e basta un po'
di buon senso per evitare situazioni spiacevoli.
LA SOLUZIONE : CRITTOGRAFIA
La crittografia é l'arte di rendere indecifrabile una comunicazione
fra due entitá, siano esse fisiche od astratte. Per rendere semplice
questo concetto useremo una semplice metafora. Ammettiamo che vogliate
spedire una lettera al vostro/a spasimante e che l'unico modo consentito
nel vostro paese sia quello di usare delle semplici cartoline (oppure immaginate
che il vostro paese decida di aprire sistematicamente ogni vostra missiva,
rendendola, in pratica, né piú né meno che una cartolina).
Chiunque sia adibito al trasporto della vostra beneamata e personale cartolina,
sará in grado di leggerne il contenuto (almeno due diversi postini
piú gli addetti degli uffici postali etc.). Questa situazione descrive
esattamente l'ambiente in cui un sistema crittografico si trova ad operare.
E' bene stabilire delle convenzioni : diremo cosí che voi sarete
il mandante, che il vostro/a spasimante sará il ricevente
e che il postino (il cattivo del momento) sará l'analista.
Notate come la presenza di quest'ultimo sia essenziale : senza di esso
non avrebbe senso attivare un sistema crittografico. Tale sistema renderá
impossibile all'analista leggere la lettera che avete spedito. Ammettiamo
allora che, per proteggere la privacy delle vostre informazioni, decidiate
di mettere la lettera in una cassaforte di cui solo voi e il vostro/a spasimante
conoscete la combinazione. In gergo la lettera viene definita plain
text o testo in chiaro, mentre la cassaforte con la lettera
dentro viene definita cypher text o testo cifrato. Il postino
non sará in grado di aprire la cassaforte e cosí la vostra
privacy sará salva.
Purtroppo per noi peró, l'analista é un tipo la cui forza
di volontá é devastante, ed egli userá ogni mezzo
conosciuto per aprire la cassaforte: alcuni metodi saranno molto efficaci,
altri meno. E' fondamentale peró che un buon sistema crittografico
[la cassaforte] renda costosi da realizzare i metodi piú efficaci,
cosícché non tutti gli analisti [i postini] saranno in grado
di utilizzarli.
Dopo aver introdotto l'ambiente in cui nasce e si sviluppa la crittografia,
vediamo le sue applicazioni per risolvere il problema che ci siamo posti.
In effetti, la situazione prospettata é estremamente simile alla
metafora del postino. Ritornando alla figura precedente, G sará
il mandante, E sará il ricevente, il pacchetto di dati sará
il testo in chiaro ed i nodi D, C ed A saranno gli analisti da cui ci dobbiamo
proteggere. Attraverso queste considerazioni, possiamo cominciare a parlare
dei sistemi crittografici e, soprattutto, dei metodi per sconfiggerli.
METODI SEMPLICI
La maggior parte dei metodi crittografici si basa sul fenomeno dell'esplosione
combinatorica. Vediamo come, analizzando alcuni semplici cifrari. Il primo
e piú semplice cifrario di cui si ha notizia, risale a Giulio Cesare
che lo utilizzó durante la guerra contro i Galli. Il cifrario di
Cesare richiede la scelta di un numero N compreso tra 1 e 20 : tale numero
N verrá chiamato chiave. Ammettiamo ora che si voglia cifrare
il testo "ATTACCATEALLALBA" [attaccate all'alba]. Ad ogni lettera
si associa un numero crescente A = 1, B = 2, C = 3 e cosí via, creando
una sequenza di numeri. Per il nostro testo in chiaro, la sequenza corrispondente
é 1 - 18 - 18 - 1 - 3 - 3 - 1 etc. A tale sequenza si somma N, ottenendo
una nuova sequenza : nel caso in cui N = 10 essa corrisponderá a
11 - 28 - 28 - 11 - 13 - 13 etc. Se essa contiene dei numeri maggiori di
21, si sottrarrá proprio 21 a questi ultimi, ottenendo la sequenza
finale. Nel nostro caso essa sará 11 - 7 - 7 - 11 - 13 - 13. Come
fase finale si converte di nuovo questa sequenza in lettere, ottenendo
il testo cifrato "MGGMOOMGQMVVMVNM". Schematizzando :
"ATTACCATEALLALBA" ---> N = 10 ---> "MGGMOOMGQMVVMVNM"
Per decifrare il messaggio, basterá riconvertire il testo cifrato
nella corrispondente sequenza di numeri; sottrarre a ciascuno di essi N
e sommare ai numeri negativi il numero 21. La verifica di tale proprietá
viene lasciata a voi.
Purtroppo, per un analista, trovare N risulta estremamente facile, e Cesare
se la cavó proprio perché i Galli non avevano alcuna conoscenza
di crittografia. In realtá basta provare a decodificare il messaggio
usando tutti i possibili N, che, in tal caso, sono solo 20. Un simile approccio
é comunque molto generale e viene definito "metodo della forza
bruta". Fortunatamente esso risulta impraticabile nella maggior parte
dei casi, dove le possibili combinazioni delle chiavi sono in numero estremamente
elevato.
Possiamo comunque migliorare il nostro cifrario di Cesare utilizzando una
tabella che associ, ad ogni lettera dell'alfabeto, un altra lettera dell'alfabeto.
Ad esempio A = T, B = R, C = D, D = G etc. In tal caso la chiave sarebbe
rappresentata dalla sequenza di 21 lettere TRDG... In quest'ultimo caso,
le combinazioni possibili di lettere che si possono formare sono ben 21!,
un numero elevatissimo, circa 50 miliardi di miliardi. Nonostante in questo
caso l'approccio con la forza bruta sia impraticabile, é possibile
ricavare il testo originale usando una tecnica molto semplice.
In genere, un messaggio rispetta certi schemi. Ad esempio, nella nostra
lingua, dopo la lettera H segue sempre una vocale, mai una consonante.
Oppure, esistono combinazioni particolari come GL e GN. Sfruttando la conoscenza
di questi schemi [pattern], si é in grado di risalire al messaggio
originale. Un esempio lampante di questo lo si puó trovare su ogni
"Settimana Enigmistica" nei giochi come "Il testo cifrato"
o come "Parole crociate crittografate". Questa versione del cifrario
di Cesare, in pratica conserva gli stessi pattern all'interno del testo
cifrato. Nell'esempio precedente si puó osservare come le doppie
consonanti nel testo in chiaro corrispondano a doppie lettere [non necessariamente
consonanti] nel testo cifrato. Vediamo allora come sia possibile migliorare
questa situazione.
Nel cifrario di Vigenere si utilizza come chiave K un testo di lunghezza
variabile. Al momento della cifratura, ad ogni lettera del testo in chiaro
si aggiunge la lettera della rispettiva chiave K. Ad esempio, sia K = "CRISTIANO"
e il messaggio da cifrare M = "ATTACCATEALLALBA". Allora, la
prima lettera del testo cifrato sará C + A = D, la secondo R + T
= O e cosí via, utilizzando ciclicamente le lettere di K. Il testo
cifrato sará quindi della forma "DOFTZNB...". Si puó
osservare che schemi tipici della lingua italiana come la doppia T o la
doppia C siano stati completamente eliminati nel rispettivo testo cifrato
: ció rappresenta in effetti un notevole vantaggio. Purtroppo, anche
il cifrario di Vigenere é estremamente vulnerabile, e oggi esistono
metodi piú o meno efficienti per la sua elusione. Ciononostante
ne esiste una variazione che rappresenta il sistema crittografico piú
sicuro che sia mai stati inventato : lo One-Time Pad.
L'unica differenza rispetto al cifrario di Vigenere risiede nella chiave.
Essa infatti é di lunghezza pari alla lunghezza del testo da cifrare.
E' dimostrabile matematicamente che un cifrario siffatto risulta invulnerabile,
persino contro un attacco basato su forza bruta. Ammettendo infatti che
tale metodo sia applicabile (cosa che nei casi reali é impossibile),
il trovare la chiave corrisponderebbe proprio ad indovinare il testo celato
nel codice cifrato. Facciamo un esempio : sia T = "ATTACCATE"
il testo da cifrare, e che la chiave sia ancora una volta K = "CRISTIANO".
Il testo cifrato, come abbiamo visto poc'anzi, sará proprio C =
"DOFTZNBIT". Ammettiamo ora che io voglia provare ogni possibile
combinazione di K. Tra di esse c'é senz'altro anche la chiave K'
= "CSOOCQALO". Ora, decodificando C con K otteniamo la frase
"ATTACCATE", mentre decodificandolo con K' otteniamo la frase
"ASPETTATE". In questo caso ci troviamo di fronte ad una ambiguitá
che non é possibile risolvere : quale sará la chiave esatta
? Questo perché ad ogni possibile messaggio é associata una
chiave K che potrebbe andare bene, quindi in nessun caso si puó
risalire al messaggio originale.
Lo One-Time Pad é cosí efficace e sicuro da essere stato
usato nelle comunicazioni attraverso la famosa linea rossa fra Washington
e il Cremlino durante il periodo della guerra fredda. Purtroppo la lunghezza
delle chiavi ne rende impossibile l'utilizzo in condizioni normali. In
ogni caso questo ci porta a considerare un interessante aspetto dei sistemi
crittografici : nessuno di essi, eccezion fatta per lo One-Time Pad, é
dimostrabilmente sicuro; anche se nessun attacco ha mai funzionato, non
é detto che in futuro si possa scoprire un sistema efficace ed economico
per eluderlo. Ecco perché i sitemi crittografici piú usati
sono quelli che hanno resistito piú a lungo agli attacchi degli
analisti.
METODI CONTEMPORANEI
I metodi visti nel paragrafo precedente rappresentano sistemi crittografici
elementari e per lo piú superati. I sistemi crittografici moderni
e contemporanei attingono a piene mani da conoscenze derivate da numerose
branche della matematica, prima fra tutte l'Algebra. Inoltre la loro complessitá
é cresciuta di pari passo con la loro efficacia, tanto che gli algoritmi
piú usati oggi sarebbero inapplicabili senza un computer o una qualsiasi
macchina per il calcolo automatico. Vediamone alcuni in dettaglio.
Il primo fra tutti é senza dubbio il DES, Data Encryption Standard,
introdotto negli Stati Uniti dai crittoanalisti governativi nella metá
degli anni 70. Il DES é un sistema crittografico che sfrutta chiavi
di lunghezza pari a 64-bit [8 caratteri ASCII].
Il suo sistema di funzionamento é abbastanza macchinoso. In pratica
esso espande la chiave K data in un insieme di chiavi molto piú
grande, attraverso l'uso di numerose procedure. Il testo da cifrare viene
poi suddiviso in blocchi di 64-bit (il DES, come molti altri algoritmi,
viene definito "block-based") e fatto passare 16 volte attraverso
16 diverse S-boxes, che non sono altro che funzioni che rimpiazzano il
blocco usando le precedenti espansioni della chiave K. Alla fine i vari
blocchi cifrati vengono riuniti fino a formare il testo cifrato finale.
Il DES resistette per ben vent'anni alla furia degli analisti. Purtroppo,
tre diversi attacchi risultarono fatali. Il primo, inventato da E. Biham
e A. Shamir é conosciuto come Analisi Differenziale. Esso
si basa sull'analisi dei testi entranti ed uscenti dalle S-boxes, e, ad
ogni coppia di testi esaminati, é in grado di restringere il capo
delle possibili chiavi utilizzate. E' ovvio che tali testi devono avere
delle caratteristiche ben determinate : in particolare essi devono
contenere delle ben determinate differenze, da cui la denominazione di
"differenziale". L'analisi differenziale prevede peró
l'analisi di una ingente quantitá di testi cifrati, che non sempre
risulteranno disponibili. Inoltre il DES puó essere facilmente modificato
in modo che l'analisi differenziale risulti completamente inefficace. Infatti,
per un DES da 16 round (ogni round corrisponde ad un passaggio del testo
in chiaro in una diversa S-box), occorrono circa 2^48 blocchi cifrati,
una cifra grosso modo accettabile rispetto alla forza bruta. Se incrementiamo
il numero dei round (e, conseguentemente, delle S-boxes) a 17 o 18, il
tempo necessario per applicare l'analisi differenziale diventa uguale a
quello necessario per applicare la forza bruta. Addirittura, se il numero
di round fosse pari a 19, l'analisi diverrebbe impossibile, perché
occorrerebbero piú di 2^64 blocchi cifrati diversi, cosa impossibile
perché tutti i possibili blocchi cifrati sono al piú proprio
2^64. Una piccola curiositá : ci si potrebbe chiedere come mai il
DES sia cosí resistente all'analisi differenziale; in realtá,
per stessa ammissione di D. Coppersmith dei laboratori IBM, i progettisti
del DES, al momento della sua creazione, conoscevano giá il metodo
dell'analisi differenziale; tuttavia, per un lungo periodo di tempo, i
documenti ad essa relativi vennero dichiarati Top Secret dal governo degli
Stati Uniti.
Un'altro attacco sferrato contro il DES prende il nome di Approssimazione
Lineare, introdotto nel 1993 da M. Matsui. Lo scopo di questa tecnica
analitica é quello di approssimare linearmente il funzionamento
stesso del DES. Purtroppo tale sistema é abbastanza complicato,
e quindi non verrá ulteriormente approfondito.In ogni caso l'approssimazione
lineare non é in grado di scoprire interamente la chiave, ma solo
alcune sue parti. Tuttavia, note queste parti, una ricerca con forza bruta
diventa un approccio molto piú abbordabile, visto che, per ogni
bit conosciuto, il numero delle combinazioni delle chiavi viene dimezzato.
In ogni caso, l'attacco piú grave e definitivo venne sferzato da
Micheal J. Wiener nel 1993. Il suo attacco si basava essenzialmente sulla
forza bruta. In pratica, egli progettó un CHIP in grado di provare
un determinato numero di chiavi in un certo tempo. Il costo di tale CHIP
é attualmente stimato in circa 10$. Utilizzarne uno solo risulta
ovviamente impossibile, visto che il numero di chiavi da testare é
elevatissimo ed i tempi corrispondenti sono anch'essi elevatissimi. Il
CHIP progettato da Wiener possedeva peró una caratteristica molto
importante : esso poteva essere facilemente accoppiato con altri CHIP in
modo da formare una macchina parallela in grado di provare un numero elevatissimo
di chiavi. Si é calcolato che con una spesa di circa un miliardo
di lire, si puó costruire una macchina in grado di ricostruire una
chiave K in un tempo pari a tre ore e mezza. Una macchina del genere puó
facilmente essere acquistata da una grossa azienda. Inoltre, con una macchina
da 100 miliardi di lire (una cifra spendibile da un ente governativo come
l'NSA - National Security Agency), si puó ricostruire una chiave
qualsiasi in pochi secondi.
E' ovvio che un simile CHIP poneva dei seri dubbi sul fatto che si dovesse
continuare ad usare il DES come meccanismo di cifratura, anche se in realtá
il CHIP non venne mai costruito.
Cosí la comunitá scientifica si mosse per cercare un degno
sostituto del DES. Venne proposto il cosidetto Triple-DES che consisteva
nel cifrare tre volte con il DES e con tre chiavi diverse un testo. Nonostante
questo algoritmo possa ritenersi sufficientemente sicuro, esso ha lo svantaggio
di essere in linea di massima tre volte piú lento del DES e di utilizzare
chiavi da 192-bit. Attualmente i migliori sostituti del DES sono rappresentati
dall'IDEA e dal Blowfish.
Il primo dei due é quello piú utilizzato, semplicemente perché
é stato il primo ad essere introdotto e a subire il numero piú
elevato di attacchi (ricordate quello che abbiamo detto a proposito dello
One-Time Pad). Esso venne proposto da due scienziati svizzeri dello Swiss
Federal Institute of Technology of Zurich in collaborazione con la Ascom
Communications inc. : il Dr. X. Lai e il Prof. J. Massey. Il suo meccanismo
é molto diverso dal DES e sfrutta chiavi di soli 128-bit. Attualmente
nessun attacco é stato in grado scalfirne la sicurezza, tanto che
la Ascom sponsorizza una gara con un grosso premio che verrá assegnato
alla prima persona in grado di decifrare un testo cifrato con IDEA. Notate
che una chiave da 128-bit é sufficiente per mettere al tappeto la
macchina di Wiener. Essa infatti impiegherebbe circa 2^64 anni per provare
tutte le possibili chiavi. Una stima ci dice che, qualora si fosse in grado
di costruire una macchina anche qualche miliardo di volte piú potente
della macchina di Wiener, e anche ammettendo che la velocitá dei
microprocessori raddoppiasse ogni 18 mesi, si impiegherebbe circa un secolo
per trovare la chiave di un singolo messaggio, una stima che mette completamente
fuori discussione un attacco con forza bruta.
Il secondo dei candidati successori del DES é il Blowfish, presentato
per la prima volta da B. Schneier sulle pagine del noto Dr. Dobb's Journal
nel '94. Il suo funzionamento é per certi versi simile al DES :
nel Blowfish le chiavi da 448-bit vengono espanse in numerose altre chiavi
in modo da formare di nuovo delle S-boxes anche se di struttura differente
rispetto al DES. Bruce ha recentemente presentato i risultati di una gara
di crittoanalisi sponsorizzata dal Dr. Dobb's Journal : i rusltati ottenuti
sono incoraggianti e la maggior parte degli attacchi presentati sono in
grado di ricostruire solo chiavi molto piccole, oppure assumono che le
S-boxes siano note. Comunque sembra che, anche per il Blowfish, la sicurezza
sia garantita.
Probabilmente non ci sará un vincitore. La Ascom supporta pesantemente
l'IDEA, progettando CHIP crittografici molto potenti e fornendo assistenza
agli sviluppatori. Purtroppo l'algoritmo IDEA é stato brevettato
e il suo utilizzo per scopi commerciali é sottoposto al pagamento
di una royality. D'altro canto il Blowfish é completamente gratuito,
ma l'assistenza fornita da Bruce Schneier é esigua e gli sforzi
compiuti per testarlo sono ancora troppo pochi. Ai posteri l'ardua sentenza.
CHIAVI PUBBLICHE
Analizziamo in questo paragrafo una classe di algoritmi crittografici
molto interessanti, perché risolvono il problema della sicurezza
in un modo completamente diverso da ogni altro tipo di sistema crittografico.
In un sistema crittografico tradizionale, é previsto che il mandante
e il ricevente posseggano una copia della chiave di cifratura. Questa caratteristica
non sempre é desiderabile. Ammettiamo infatti che dobbiate spedire
un messaggio cifrato ad una persona che si trova dall'altro lato del globo.
Come fate per scambiarvi la chiave da utilizzare ? I telefoni possono essere
intercettati, e di usare Internet non se ne parla neanche. Ammettendo che
siate in grado di trasmettere con sicurezza la chiave da utilizzare (questo
é possibile, ma solitamente piú il canale di comunicazione
é sicuro, piú esso é costoso), chi vi dice che un
giorno il vostro amico non decida di rendere pubblica la chiave che magari
voi avete utilizzato anche con altri amici ? Si tratta quindi di un problema
grave.
Per risolverlo, nel 1976, W. Diffie e M. Hellman, definirono uno schema
che oggi va sotto il nome di "crittografia a chiave pubblica".
Questo sistema prevede tre condizioni :
- La chiave di cifratura e quella di decifratura sono diverse. Esse vengono
chiamate, rispettivamente, chiave pubblica e chiave privata.
- E' difficile ricavare la chiave privata dalla chiave pubblica e dal
testo cifrato
- E' facile cifrare e decifrare il messaggio in esame
Ritornando alla metafora del postino, dovete immaginare che il mandante
chiuda il messaggio da spedire all'interno di una cassaforte utilizzando
una chiave presa da un archivio pubblico (una specie di elenco telefonico).
A quel punto la cassaforte puó essere aperta soltanto da chi é
in possesso della chiave di decifratura. Neanche chi ha scritto il messaggio
é piú in grado aprire tale cassaforte.
I due matematici peró non diedero alcuna indicazione circa un metodo
concreto per realizzare un tale sistema. Fortunatamente per noi, ci pensarono
nel 1978 tre scienziati, R. Rivest, A. Shamir (quello dell'analisi differenziale)
e L. Adleman. Il loro sistema crittografico é conosciuto come "sistema
a chiave pubblica RSA", dal nome dei tre scienziati.
Non spiegheremo in dettaglio il funzionamento dell'RSA, in quanto richiede
la conoscenza di rami della matematica molto particolari, ma diremo soltanto
che esso si basa sull'impossibilitá di fattorizzare un numero molto
grande nei suoi fattori primi. Le chiavi utilizzate nell'RSA sono infatti
molto lunghe, solitamente di 1024-bit e su esse vengono compiute delle
operazioni molto particolari che richiedono un notevole sforzo computazionale.
L'RSA infatti presenta una complessitá molto superiore a qualsiasi
altro algoritmo di cifratura e questo fattore ne limita fortemente la diffusione.
E' attualmente impensabile di sfruttare l'RSA per crittografare interamente
files o sessioni Internet. Tuttavia esso fornisce un ottimo sistema per
la distribuzione delle chiavi nei sistemi crittografici tradizionali. Questo
peró lo vedremo piú avanti.
STEGANOGRAFIA
No, non é una parolaccia :-) Dietro questo nome si cela una tecnica
che permette di nascondere ad un qualsiasi osservatore il fatto che in
un dato momento stia avvenendo una comunicazione, non necessariamente cifrata,
tra due entitá. Per capire esattamente cosa essa significhi, descriveremo
il modo con cui gli egiziani se ne servivano.
In tempo di guerra, per comunicare le proprie decisioni, il faraone ordinava
agli scriba di tagliare a zero i capelli di uno schiavo, e di scrivere
sulla sua testa calva il messaggio da spedire ai propri generali. Si aspettava
poi che allo schiavo ricrescessero i capelli che andavano cosí a
nascondere il messaggio. Lo schiavo veniva poi mandato a destinazione.
Chiunque lo avesse osservato, non avrebbe mai immaginato che fosse latore
di messaggi di importanza vitale. In questo modo egli era in grado di passare
inosservato giungendo felicemente a destinazione, dove i generali tagliavano
di nuovo i capelli dello schiavo e leggevano gli ordini del proprio faraone.
Questa tecnica venne poi perfezionata nei secoli e vennero impiegati i
mezzi piú strampalati : gli inchiostri simpatici ad esempio vennero
largamente utilizzati per tali scopi. Provate a scrivere un messagio con
succo di limone su un foglio di carta : quest'ultimo apparirá a
chiunque come un normalissimo foglio bianco che, posto sotto l'azione del
calore, rivelerá il messaggio nascosto. Risultati migliori comunque
si ottengono utilizzando inchiostri al cobalto. Metodi piú sofisticati
prevedono l'uso dei cosidetti "micropunti fotografici"
nascosti all'interno di una fotografia. In tali piccolissimi punti, impercettibili
all'occhio umano, si possono nascondere messaggi segreti anche molto sofisticati.
Potevano i computer mancare all'appuntamento con la steganografia? Certamente
no, tanto piú che essa si adatta perfettamente alla teoria dei codici
che attualmente é alla base dei calcolatori elettronici. Vediamo
come. Come sappiamo, ogni informazione contenuta nel nostro computer é
rappresentanbile sottoforma di sequenze di numeri da 8-bit. Ammetiamo ora
di prendere in considerazione il numero 76, che puó essere scritto
come 01001100 in base due. Cambiamo ora il bit che si trova piú
a destra. La sequenza binaria cambierá in 01001101 corrispondente
al numero 77. Adesso cambiamo invece il bit che si trova piú a sinistra
: la sequenza corrispondente sará 11001101, ovvero pari a 204. Come
vediamo, nonostante in entrambi i casi sia stato cambiato un solo bit,
il risultato ottenuto é estremamente diverso : un leggero cambiamento
nel primo e un evidente cambiamento nel secondo. In realtá il cambiamento
dipende dalla posizione del bit in esame secondo una relazione esponenziale.
Questa considerazione fá si che si possa cambiare il valore di gruppi
di bit nelle posizioni piú a destra senza stravolgere il signifcato
del numero.
Questo si rivela estremamente proficuo nel caso delle immagini o dei suoni.
Nelle immagini, un cambiamento degli ultimi due bit nel colore di un pixel
(nel caso di immagini a scala di grigi o True Color) non cambia signifcativamente
il colore del pixel stesso, che, all'occhio umano, si presenterá
con le medesime caratteristiche. Cosí resta definita una tecnica
che permettere di nascondere in una immagine una sequenza qualsiasi di
bit : se il messaggio da spedire é lungo N bytes, é essenziale
che l'immagine sia composta di almeno 4N bytes. Ad esempio, confrontate
le seguenti immagini :

L'immagine originale

L'immagine steganografata
L'immagine superiore é un'originale tratta da un PhotoCD, mentre
quella inferiore contiene un'immagine JPEG della famosa modella Kate
Moss. Se non ci credete, provate ad usare S-Tools 4.0 [vedi dopo] sulla
seconda immagine, selezionando l'algoritmo IDEA e utilizzando la parola
"beta" come password. Le due immagini comunque sono praticamente
uguali.
Un discorso analogo vale per i suoni campionati. Nelle codifiche a 16-bit,
addirittura é possibile cambiare i primi 8 bit di destra senza cambiare
significativamente la qualitá del suono campionato. E' cosí
possibile fare una stima della bontá del mezzo steganografico (cioé
delle immagini e dei suoni). Se infatti N é il numero di bit di
una unitá staganografica (ad esempio, 8 bit nel caso delle immagini
e 16 nel caso dei suoni) ed M il numero dei bit steganografati (2 nel caso
delle immagini e 8 nel caso dei suoni), la seguente formula ci fornisce
una stima della bontá del mezzo steganografico :
b = ( 2^N / 2^M ) * ( M / N)
Tale formula associa il valore b = 16 per le immagini e b = 128 per
i suoni. Come vediamo il suono é un mezzo steganograficamente migliore
delle immagini. Altri mezzi steganografici si rivelano, ad esempio, lo
spazio non utlizzato dei dischetti e degli HD, oppure gli spazi di giustificazione
nei files testuali.
Purtroppo la situazione non é cosí rosea come sembra. Attualmente
infatti le immagini ed i suoni vengono distribuiti in formati che prevedono
una leggera perdita di definizione a fronte di un piú elevato rapporto
di compressione. Per le immagini non-broadcast ad esempio, il formato piú
diffuso é il JPEG che sfrutta proprio questo tipo di algoritmi.
In questo formato, i pixel vengono trasformati per assumere una maggiore
omogeneitá. Questo risultato é ottenuto prevalentemente modificando
i bit piú a destra del pixel, cioé proprio quelli interessati
dalle tecniche di steganografia. Attualmente si stanno conducendo numerose
ricerche per utilizzare anche immagini JPEG, ma purtroppo ci troviamo ancora
in una fase sperimentale. Per il mondo UNIX peró esiste giá
un programma, il JSTEG, che é in grado di nascondere files all'interno
di immagini JPEG. Il suo funzionamento é in realtá molto
semplice e si basa sul fatto che la codifica JPEG, da un certo punto in
poi, diviene lossless (ovvero, senza perdita di informazione). Vediamo
questo schema :

Come vedete, si parte dall'immagine BitMap non compressa e la si trasforma
utilizzando una procedura matematica chiamata "Discrete Cosine Transform"
- DCT. L'immagine trasformata viene poi filtrata, ponendo a zero quanti
piú pixel possibile. A questo punto si utlizza la compressione di
Huffman (una codifica non distruttiva) per comprimere i dati. Il JSTEG
modifica l'immagine filtrata cambiando l'ultimo bit a destra con un bit
del messaggio da nascondere. Se visualizziamo l'immagine steganografata,
essa apparirá esattamente come era all'inizio, ma utilizzando il
JSTEG al contrario si potrá estrarre il messaggio nascosto. I vantaggi
sono ovvi, e sembra addirittura che l'impatto sull'immagine originale sia
addirittura minore rispetto ai risultati su formati lossless tradizionalmente
usati come il GIF o il BMP. Questo perché si tende a modificare
canali visivi a cui l'occhio é poco sensibile. Purtroppo il JSTEG
modifica un solo bit su otto, quindi ha una capacitá dimezzata rispetto
agli altri formati. Questo perché si deve mantenere un livello accettabile
di omogeneitá fra i dati o si rischia di rendere inefficace la codifica
di Huffman o di modificare troppo l'immagine originale.
IL SOFTWARE
In questo paragrafo non parleró degli applicativi di crittografia
commerciali perché, a differenza di quello che si potrebbe pensare,
gli algoritmi utilizzati nei programmi commerciali sono molto semplici
e normalmente possono essere violati con poco sforzo, alcuni addirittura
usando carta e penna. Questo per una serie di motivi. Il piú importante
riguarda l'attuale legislazione statunitense in materia di esportazione
d'armi. Tale campo é regolato dalla famigerata legge denominata
ITAR - International Trafic in Arms Regulation. In pratica questa vieta
qualsiasi esportazione illegale di armi al di fuori degli Stati Uniti.
Purtroppo per noi peró, l'ITAR definisce i programmi di crittografia
"armi non esportabili" qualora la complessitá degli algoritmi
utilizzati sia troppo elevata. In pratica, si vieta l'utilizzo di un qualsiasi
algoritmo di crittografia che sia basato su chiavi superiori a 40
bit (recentemente tale limite é stato portato a 56 bit). E' possibile
accorgersi di quanto sia restrittiva la legge osservando le varie etichette
che indicano l'assenza di un qualsiasi algoritmo di crittografia all'interno
del programma. Questo si riflette in una blanda protezione da parte di
programmi che invece contengono un qualsiasi algoritmo crittografico.
Il discorso é invece diverso per i programmi freeware che vengono
in maggioranza prodotti in stati diversi dal Nord America (infatti anche
il Canada si é dotato di una legislazione molto severa in questo
senso).
Il programma di crittografia per eccellenza é il Pretty Good Privacy (PGP)
di Phil Zimmerman. Lo scopo principale di PGP é quello di permettere
la trasmissione cifrata di messaggi di posta elettronica fra utenti diversi
attraverso Internet. In realtá le operazioni possibili sono molteplici.
Il PGP utilizza due algoritmi di crittografia : il sistema a chiavi pubbliche
RSA e l'IDEA. Il suo funzionamento é molto semplice. Ammettiamo
che l'utente A voglia spedire all'utente B un messaggio. PGP cifra tale
messaggio utilizzando l'IDEA e una chiave K generata casualmente. Come
fare peró a spedire all'utente B la chiave K da utilizzare per decifrare
il messaggio (ricordiamo che l'IDEA é un algoritmo che utilizza
la stessa chiave per cifrare e decifrare il messaggio) ? Il PGP risolve
brillantemente il problema utilizzando l'RSA. Infatti, l'utente A fornisce
a PGP la chiave pubblica P dell'utente B che la cifra utilizzando questa
chiave e la spedisce insieme al messaggio. Notate che, in teoria, si sarebbe
potuto utilizzare direttamente l'RSA per cifrare l'intero messaggio. In
pratica peró, poiché la complessitá dell'RSA é
troppo elevata per permetterne un uso intenso (i file da cifrare potrebbero
essere molto lunghi), soprattutto se messo in relazione con l'IDEA. Il
sistema di cifratura IDEA-RSA di PGP é riassunto dal seguente schema
:
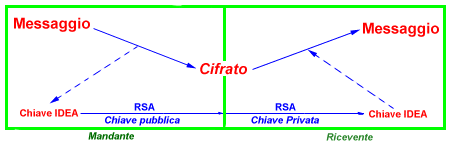
Schema di cifratura di PGP
L'RSA, per come é stato definito, permette peró un'altra
importante operazione : l'autenticazione di un messaggio. In pratica, se
il messaggio viene cifrato utilizzando la chiave privata S invece della
chiave pubblica P, si ottiene un messaggio cifrato che puó essere
decifrato utilizzando soltanto la chiave pubblica P. Se il contenuto del
messaggio é noto, allora si puó verificare che esso sia stato
cifrato solo da chi é in possesso della chiave privata S decifrandolo
con la corrispondente chiave P pubblica. Ma allora, se solo chi é
in possesso di S puó aver cifrato il messaggio, allora possiamo
star tranquilli che il messaggio é "autentico". E' come
se l'autore del messaggio, cifrandolo con S, lo avesse firmato. PGP permette
anche questo: si puó firmare un messaggio utilizzando la propria
chiave privata in modo che chiunque possa verificarne l'autenticitá
attraverso la corrispondente chiave pubblica. Una delle applicazioni piú
frequenti di questo meccanismo é l'autenticazione degli archivi
ZIP. Il vantaggio é evidente : quando si usa un programma crittografico
si pone fiducia in esso. Tuttavia si potrebbero distribuire dei programmi
che utilizzano algoritmi crittografici meno potenti, illudendo l'utente
di una protezione elevata. Se invece si autentica l'archivio si puó
star sicuri che l'archivio che stiamo scompattando é proprio quello
originale (un eventuale "pirata" dovrebbe essere in possesso
della chiave S per autenticare il nuovo archivio).
PGP prevede comunque la creazione di archivi pubblici elettronici che contengano
le chiavi pubbliche dei vari utenti. E' importante che si dia la massima
diffusione alla propria chiave pubblica perché, se cosí non
fosse, si potrebbe applicare il seguente attacco: in pratica, l'analista
C si frappone fra A e B spedendo ad entrambi la propria chiave pubblica
facendo credere loro che si tratti invece della chiave pubblica di A o
di B. In questo modo C é in grado di intercettare e leggere ogni
messaggio spedito da A a B e viceversa.
Come potete immaginare, PGP é un programma estremamente potente,
nonostante sia totalmente freeware. Ci si puó chiedere come mai,
nonostante esso sia stato prodotto negli Stati Uniti, venga esportato in
tutto il mondo nonostante il severissimo ITAR. La risposta é che...
ció in realtá non viene proprio fatto. Infatti, attualmente,
esistono due versioni di PGP, quella statunitense e quella internazionale
che si distinguono per due motivi :
- Le versioni statunitensi non possono essere esportate dagli Stati Uniti
- Le versioni internazionali vengono prodotte e distribuiti in paesi
diversi dagli Stati Uniti. Qualora una versione internazionale venga importata
negli Stati Uniti, l'autore avverte che una sua ri-esportazione rappresenta
una violazione grave dell'ITAR.
Nonostante ció le due versioni sono assolutamente equivalenti
e possono essere utilizzate indifferentemente.
Un'ultima informazione : PGP é disponibile, in maniera nativa, su
DOS, Macintosh e tutti i sistemi UNIX. Purtroppo non esiste una versione
specifica per Windows. Comunque, per questo sistema operativo sono disponibili
numerosi front-end che si interfacciano con PGP per DOS e con numerosi
programmi di posta elettronica, come ad esempio Eudora.
Un'altro fronte molto attivo degli applicativi di crittografia é
il chat. In realtá su Internet sono diffusi due tipi diversi di
chat: IRC e DCC. Il primo [Internet Relay Chat], prevede che l'utente
si connetta ad un server che si occupa di metterlo in comunicazione con
gli altri utenti ad esso collegati, tutti quanti insieme. In realtá,
attraverso IRC é possibile aprire anche comunicazioni private, che
tuttavia saranno comunque registrate dal server che ha messo in connessione
i due utenti.
Il secondo tipo di chat, il Direct-to-Client Chat, prevede che due utenti
entrino in comunicazione diretta fra loro, senza che i messaggi scambiati
passino attraverso un server apposito. Questo tipo di comunicazione é
solitamente ritenuto molto piú sicuro di IRC, perché il routing
compiuto dai paccheti di messaggi tra due utenti é molto difficile
da intercettare. Tuttavia, per ottenere il massimo della sicurezza, sarebbe
auspicabile un sistema che fosse in grado di cifrare i messaggi in tempo
reale. Purtroppo, né IRC ne DCC permettono di fare questo e i programmi
che cifrano le sessioni sono limitati a protocolli di chatting proprietari,
non definiti attraverso lo standard mondiali, come RFC. E' per tali motivi
che non tratteremo ulteriormente questo tipo di programmi, che tra l'altro,
utilizzano algoritmi crittografici poco potenti e che quindi sarebbero
di scarsa utilitá.
L'ultima serie di programmi che andremo ad esaminare riguarda la steganografia.
Uno dei programmi piú efficaci in tal senso é l'S-TOOLS 4.0
per Windows. Il programma é un grado di nascondere, all'interno
di immagini GIF e BMP e di samples WAV (non-compressi) un qualsiasi insieme
di files. S-TOOLS é in grado anche di crittografare preliminarmente
i files nascosti attraverso l'uso di vari algoritmi, tra cui spicca l'IDEA.
Basterá inventare una password da ricordare quando si vorrá
estrarre il file dall'immagine o dal campione audio. S-TOOLS é dotato
di una comoda interfaccia Drag&Drop e di visualizzatori automatici
di suoni e immagini. Inoltre, nel caso del formato GIF, il programma é
in grado di eseguire automaticamente la riequilibratura dei colori attraverso
l'uso di vari algoritmi di dithering come il Floyd-Steinberg.
Un'altro programma di steganografia é il JSTEG, l'unico programma
in grado di nascondere files all'interno di immagini JPEG. Purtroppo il
programma é ancora in fase di sperimentazione e attualmente é
disponibile solo in formato sorgente compilabile direttamente per UNIX.
Non si hanno notizia di porting su altre piattaforme.
Altri programmi degni di nota :
- PGP Stealth: Lavora in congiunzione con PGP per rendere i messaggi
cifrati attraverso RSA puro rumore casuale e nascondere i messaggi all'interno
di immagini.
- Steganos 1.4: E' in grado di nascondere i messaggi all'interno di
files ASCII
- EZStego Java: L'unico programma di steganografia scritto in JAVA
- Stego: Un ottimo programma di steganografia per Macintosh
- S-Tools 3.0: La precedente versione di S-Tools, in grado di nascondere
files all'interno dello spazio vuoto dei floppy. S-Tools 4.0 non implementerá
piú questa caratteristica, essendo stato progettato anche per Windows NT
che, come tutti sanno, non permette la scrittura diretta su HD e floppy
per motivi di sicurezza
La Seven
Locks maniene una lista aggiornata e un archivio di tutti i programmi
di steganografia : fateci un salto, sono tutti completamente freeware.
LINK INTERESSANTI
I link sulla crittografia e sulla steganografia sono moltissimi. Eccone
un elenco e una breve descrizione :
|
Ascom International inc.
|
Il sito della societá che detiene i diritti di brevetto per
l'algoritmo IDEA. Vi si possono trovare link sull'IDEA, una descrizione
dell'algoritmo in fromato Word, informazioni sulle licenze e fonti di informazioni
come mailing list sullo stato degli attacchi contro questo algoritmo. Sembra
che a breve sará disponibile anche un sito
italiano, anche se, al momento della stesura dell'articolo, non sembra
essere stato ancora attivato. |
|
Underground Organization
|
Un'organizzazione senza scopo di lucro impegnata nella libera ricerca
e diffusione in numerosi campi dell'informatica. Possegono uno dei piú
grossi archivi su programmi per proteggere il proprio computer e papers
suglli algoritmi di crittografia. |
|
Dr.Dobb's Journal
|
Non ha bisogno di commenti. Nei suoi archivi si trova di tutto, anche
i sorgenti del Blow Fish. |
|
SevenLocks Software
|
La SevenLocks mantiene un archivio dei piú diffusi programmi
di steganografia disponibili per le varie piattaforme. |
|
RSA Data Security inc.
|
La societá detentrice dei diritti dell'RSA. |
|
TUCOWS
|
Uno dei siti piú frequentati su Internet. Contiene un numero
enorme di programmi sulla crittografia, soprattutto front-end per PGP e
programmi di Chat cifrato. |
|
VOL ftp
|
Dateci un'occhiata. Contiene una ventina di programmi sulla crittografia
e sulla protezione dei PC in genere. Contiene anche S-TOOLS 4. |
|
sci.crypt
|
E' il newsgroup per eccellenza riguardo a problemi di crittografia
e simili. |
CONCLUSIONI
Il problema della sicurezza su Internet é preoccupante. Ma ancor
piú preoccupante é la leggerezza con cui sono affrontati
questi argomenti da parte del grande pubblico. Internet é anarchia
allo stato puro, ma gli utenti dovrebbero tutelarsi da qualsiasi illecito
che potrebbe danneggiarli. Sarebbe auspicabile che i provider si dotassero
di una "carta dei diritti" dell'utente, che almeno ne regoli
il comportamento nei confronti di questi ultimi e, soprattutto, porti alla
luce tutti i problemi connessi con la sicurezza. L'unica che in tal senso
sta sviluppando una condotta simile é MC-link
che ormai da alcuni mesi ha reso disponibile on-line una "mega-FAQ" sugli
argomenti piú disparati, tra cui anche riguardanti la problematica
della sicurezza. I consigli che posso darvi sono due : non fatevi prendere
dal panico ma siate prudenti in quello che fate. Spero che l'articolo abbia
soddisfatto le vostre curiositá e i vostri dubbi; se volete continuare
a parlarmene (il mio indirizzo é incluso nella pagina di redazione), lo faró con molto piacere. A presto.
Cristiano Paris è raggiungibile su Internet tramite la redazione
|












